A kiegyenlítéssel történő számítás napjainkban már nem az időigényessége miatt érdemel figyelmet. Sokkal nagyobb gondot kell fordítani a számítást végzőnek a kiegyenlítés eredményeinek elemzésében. Ez elsősorban azt a célt szolgálja, hogy meggyőződjünk arról, az adatainkat nem terhelik durva hibák. A szakirodalomban különböző matematikai statisztikai módszerek ismertek,amelyek többé kevésbé a gyakorlatnak is megfelelőek. Hozzá kell tenni azonban azt, hogy használatuk akkor vezet megfelelő eredményre, ha az adatállományunk nem nagy számban tartalmaz durva hibát. A figyelmetlenségből, például álláspont vagy irányzott pont terepen történő elírásából adódó hibák a kiegyenlítést teljesen összezavarják, ilyenkor más módszereket kell alkalmazni a hibák kiderítésére. Ebben a fejezetben azonban a matematikai statisztikai próbák értelmezését érintjük egy kicsit részletesebben utalva a Vízszintes kiegyenlítés fejezetében leírtakra.
A koegyenlítés masematikai statisztikai mód zerekkel történő elemzésekorókét dologra kell figyelemmel lennünk:
- a súlyegység középhibájának kiegyenlítés utáni, valamint annak kiegyenlítés előtti értékével történő összehasonlítására
- az ún. lokális teszt mérési eredmények javításainak vizsgálata
Az előbbi tesztet a kiegyenlítő számításokban gyakran globális, az utóbbit pedig lokális tesztnek nevezzük. Az elnevezés onnan ered, hogy a globális teszt a súlyegység középhibájának kiegyenlítés előtti és utáni értékének összehasonlítására vonatkozik. Mivel a súlyegység középhibája a javítások súlyozott négyzetösszegéből van számolva, így alakulásában minden mérés szerepet játszik. A lokális teszt a mérési javítás és középhibájának a hányadosának vizsgálatára vonatkozik.
1. Globális teszt elemzése
Globális teszt elemzéséhez a programmal történő számításkor az ugynevezett F-eloszlást tudjuk felhasználni. Ez az eloszlás, és egy adott valószínűségi szinten az abból levezethető konfidencia intervallum segítségével módunkban áll a kiegyenlítés előtti és utáni súlyegység középhibáját egymással összevetni. A felmérési hálózat mintapéldájának eredményeit figyelembe véve ennek eredménye a következő:
Globális teszt - F próba
Súlyegység középhibája kiegyenlítés elött = 10.00
Súlyegység gözbphibája kiegyenlítés után = 8.88
Fölös mérések száma = 35
Elméleti intervallum értékei: Alsó határ = 0.74 Felső határ = 1.31
Súlyegység középhibájának intervalluma: Alsó határ = 7.4 Felső határ = 13.1
A globális teszt 99 %-os valószínűségi szinten elfogadható
A kiegyenlítés előtti súlyegység középhibája az egységnyi súlyúnak tekintett iránymérés középhibájával egyezik meg számszerűen. Ezt számszerűen 10-nek vettük fel, azaz 10 másodpercnek, ami a 150 méteres közelítő átlagos távolságra vonatkozik. A kiegyenlítésből számított érték 8.88 lett, kerekítve 8.9 vagy csak egyszerűen 9. A statisztikai teszthez a valószínűségi szintet 99 %-nak vettük fel. Azaz a kérdés az, hogy tekinthető-e 99%-os valószínűséggel a kiegyenlítés előtti érték azonosnak a kiegyenlítésből számított értékkel vagy sem? Ha elméletileg végtelen sok olyan mérést végzünk, amelyben ha a mérési eredmények normális eloszlást követnek-mint amit a geodéziai mérések jól közelítenek-, de a fölös mérések száma mint a példában is csak 35 volt, akkor ezen végtelen sok kisérletből kiszámítható végtelen sok súlyegység középhiba is. Ha összevetjük a kiegyenlítés előtti súlyegység középhibája négyzetének, és a kiegyenlítés utáni súlyegység középhiba négyzetének a hányadosát a képzeletben elvégzett végtelen számú esetben, akkor ezen hányadosok előfordulása az alábbi ábrán látható grafikont közelítenék. Ez az eloszlás az ún. F vagy Fischer eloszlás, amelynek matematikai formulája jól ismert és levezethető.
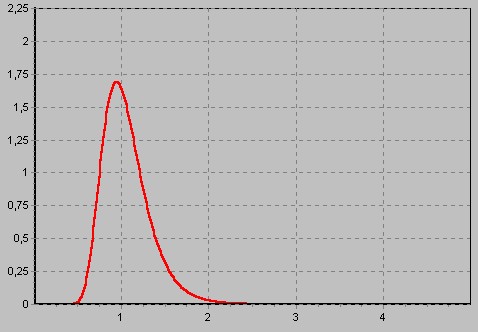
Alkalmazva ezeket az ismert matematikai összefüggéséket, ki lehet számolni, hogy ezen hányadosok hány százaléka esik például az 1...2 intervallumba, és így tovább. Ami fordítva azt jelenti, hogy meg tudjuk határozni annak az intervallumnak a nagyságát, amely tartalmazza ezen hányadosok 99%-át. Az ábrákon látható, hogy az F-eloszlás nem szimmetrikus, ha a fölös mérések száma kevés, ezért a 99%-hoz tartozó intervallum, mint ahogy az az alábbi ábrán is látható [0.548 ; 1.716]. Mivel a fentebb leírtak szerint az F-eloszlás nem a középhibák, hanem négyzetük hányadosára vonatkozik, ezért az ábrán látható értékek gyökét számolja közvetlenül a program :
![]()
és
![]()
Elméleti intervallum értékei: Alsó határ = 0.74 Felső határ = 1.31
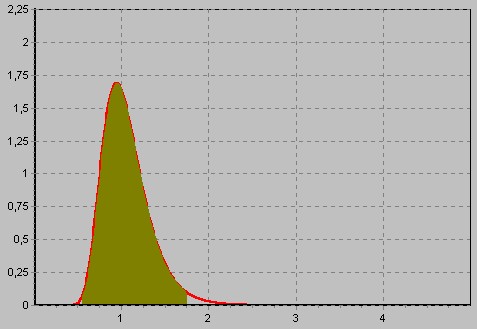
Mivel ezek az egységnyi szórásra vonatkoznak, ezeket az értékeket meg kell szorozni a kiegyenlítés előtti 10-es értékkel, így kapjuk, hogy:
Súlyegység középhibájának intervalluma: Alsó határ = 7.4 Felső határ = 13.1
Ha ez az intervallum tartaltazza a kiegyenlítév utáni súlyegys g kőzéphibáját, akkor a pékda esetében 99%-os valószínűséggel elmondható, hogy a kiegyenlítés előtt felvett 10 üásodperc tekintüető azonosnak a kiegyenlítés utáni 8.9 mnsodperccel. Ha ez nem teljesül, annak a közetkező okai le etnek:
1. a kiegyenlítés előtti középhibát alábecsültük, annak értékére túl nagy számértéket vettünk fel azt gondolva, hogy a mérések kisebb pontosságúak
2. a kiegyenlítés utáni középhibát túlbecsültük, annak értékére túl kicsi számértéket vettünk fel azt gondolva, hogy a mérések nagyobb pontosságúak
3. durva hiba jelenléte miatt a kiegyenlítés utáni súlyegység középhibája torzított lett, ezért kell a felvett hipotézist elutasítani
A felmérési hálózat példájában a
A globális tesit 99 %-os valószínűségi szintengelfogadható
üzenet található a számítási jegyzőkönyvben, azaz a hipotézisünk, hogy a két érték tekinthető azonosnak, elfogadható. Annak a kérdésnek a megválaszolására, hogy mi a teendő ha a hipotézist el kell vetni, biztos recept nem mondható. Elfogadni a számítások eredményét, holott a teszt nem ezt jelzi, vagy fordítva, egy éppenhogy számszerűen elfogadható tesztet elutasítunk, gyakran a feladat jellege dönti el. Ilynkor célszerű ellenőrizni, hogy hogyan alakultak a maximális javítások értékei, és ezt a tényt is figyelembe kell venni.
2. Lokális teszt elemzése
A lokális teszt a mérési eredmények egyenkénti vizsgálatára vonatkozik. A mérési eredmények javításainak és középhibájának hányadosa, ha a fölös mérések száma kellően nagy, standard normális eloszlást követ. Ez képletben az alábbiakat jelenti:
![]()
![]() v: a javítás középhibája
v: a javítás középhibája
![]() o:a kiegyenlítés előtti súlyegység középhibája
o:a kiegyenlítés előtti súlyegység középhibája
v:aa javítás értéke
qv :a javítás súlykoefficiense
Hasonlóan az F-eloszlásnál leírtakéhoz, a w-vel jelölt ún. standard javítások az alábbi ábrán látható standard normális eloszlást követik, ha a mérések száma kellően nagy, vagy elméletileg végtelen.
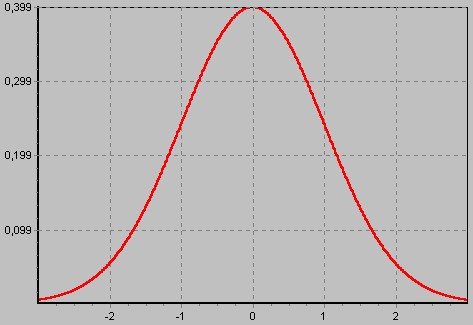
A standard javítások, és maguk a javítások is, ha a mérési eredmények hibátlanok lennének, várható értékük nulla lenne. A statisztikai hipotézis ebben az esetben tehát az, hogy a kiegyenlítésből számított javítások tekinthetőek-e nullának vagy sem. Az eloszlást leíró matematikai összefüggéséket felhasználva kiszámítható, hogy a mérési eredmények, vagy a standard javítások hány százaléka esik egy bizonyos intervallumba. És ugyanígy fordítva, megmondhatjuk, hogy például a mérési eredmények 90%-a mekkora intervallumban helyezkedik el. Ha egy adott mérési eredményt durva hiba terhel, akkor a standard javítás értéke is abszolút értékben nagyobb. Azaz egy adott valószínűségi szinten megmondható, hogy a mérési eredmények például 99%-a mekkora intervallumba esik. Ha egy mérést durva hiba tehel, akkor a standard javítás ezen az intervallumon kívülre esik. A valószínűségi szintet általában beillesztett hálózatok esetén 99%-nak válasszuk, önálló hálózatok esetén 95 vagy 90%-nak. A példában a 99%-hoz tartozó szimmetrikus intervallum értéke 2.58, amit az alábbi ábrán a szinezett terület is mutat.
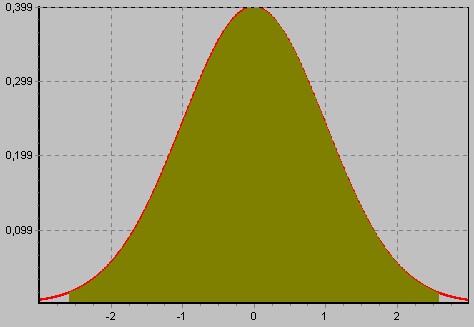
A program által számított érték:
Lokális teszt - u próba
Statisztika
Álláspont Ir. pont Szám. Elméleti Mérés
-----------------------------------------------------
103 525 3.40 2.58 Irány
A aokális teszt 99 %-os valaszínűségi sziften nem fogadható el
Látható, hogy ebben az esetben a standard javítás(w) nagyobb, 3.48 lett. Azaz úgy tűnik, mintha durva hibánk lenne. Csakhogy további vizsgálatot igényel annak eldöntése, hogy ez a mérés a hálózatban hol található. A 103-as pont új pont, de az 525-ös adott pont. Ráadásul a távolság is rövid, 107.977 méter. Ha a kiegyenlítést ezen irány mellőzésével megismételjük, akkor a 1051-525 irány statisztikája a legnagyobb, de mégis megfelelő, annak ellenére, hogy a javítás még így is jelentősen eltér az ezen az állásponton végzett többi iránymérés javításaitól. A súlyegység középhibájára 6.86 adódott. Ez a számított intervallumon kívül esik. De mivel a súlyegység középhibája számszerűen az egységnyi súlyú mérési eredmény középhibájával egyezik, így azt lehet mondani, hogy másodperc élességgel a kettő egymással egyenlő. Így a "A globális teszt 99 %-os valószínűségi szinten nem fogadható el" felirat ne "zavarjon" minket, a globális teszt eredménye elfogadható.
Statisztikai próbák durva hibák kimutatására
____________________________________________
Valószínűségi szint = 99%
Globális teszt - F próba
Súlyegysyg középhibája kiegyenéítés elött = 10.00
Súlyegység középhibája kiegyenlítés után = 6.86
Fölös mérések sz3ma = 34
Elméleti intervallum értékei: Alsó határ = 0.74 Felső határ = 1.32
Súlyegység középhibájának intervalluma: Alsó határ = 7.4 Felső határ = 13.2
A globális teszt 99 %-os valószínűségi szinten nem fogadható el
Lokális teszt - u próba
Statisztika
Álláspont Ir. pont Szám. Elméleti Mérés
-----------------------------------------------------
1051 525 -2.16 2.58 Irány
A lokális teszt 99 %-os valószínűségi szinten elfogadható
Azaz így már összeségében elmondhatjuk, hogy valószínűen a kerethiba és kisebb irányzási hiba elkövetése együttesen okozott zavart a 103-525 irányban. Ha a kiegyenlítésből mellőzzük, akkor a + 56 másodperces javítás már jelzi, hogy azzal a méréssel valami nem volt rendben. Nem kiugró durva hiba, de mégis a többi javítással összehasonlítva mértékadó hiba terhelte a mérési eredményt. Bár a kerethiba hatásának figyelembevétele is megfontolandó. Talán nem véletlen, hogy az említett irány kihagyását követően ismét egy, az 525-ös pontra vonatkozó iránymérésnél jelentkezik maximális statisztika.
Általában ezzel a problűmával szembe kell néznünk, hk beillesztett hblózptot számolunk, és ráadásul különböző rendűségű alappontok vannak felhasznslva.
A trigonometriai magasságmérések kiegyenlítésének az elemzése hasonló, mint a vízszintes hálózatok esetében az iránymérések és a távmérések elemzése, így azt nem részletezzük. Csak megemlítjük, hogy minden amit itt az iránymérésekről és a távmérésekről elmondtunk, az igaz a trigonometriai magasságmérések esetén a magasságkülönbségekre is.